高斯函数,解析与应用概览

揭秘高斯函数：数学世界的“钟形曲线”奇遇记

亲爱的读者们，你是否曾在数学的海洋中迷失方向，被那些复杂的公式和理论搞得头昏脑胀？今天，就让我们一起揭开一个神秘而有趣的数学函数——高斯函数的神秘面纱，看看它是如何成为数学世界中的“钟形曲线”奇遇记的。

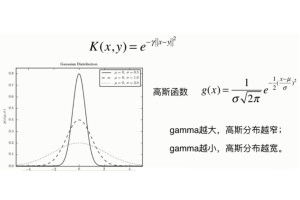
一、高斯函数：数学界的“钟形曲线”

高斯函数，又称正态分布函数，它的图形在数学上呈现为一条对称的钟形曲线。想象你站在一座钟的下方，抬头仰望，那高耸的钟楼就像一个完美的钟形，这就是高斯函数的形状。它以均值为中心，左右对称，随着距离均值的增加，曲线逐渐变得扁平，最终消失在无穷远处。

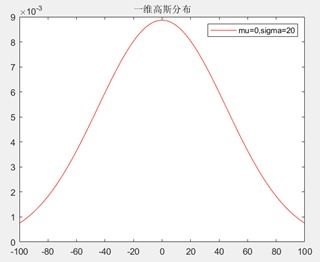
二、高斯函数的诞生：从大数学家高斯的故事说起

高斯函数的名字来源于德国著名数学家约翰·卡尔·弗里德里希·高斯。高斯是数学史上的巨匠，他的研究涉及了数学的各个领域。据说，高斯在很小的时候就展现出了惊人的数学天赋，他的老师甚至说：“高斯，你将来一定会成为数学家。”

高斯函数的诞生，与高斯在概率论和统计学领域的研究密切相关。他发现，许多自然现象都服从正态分布，而正态分布的密度函数就是高斯函数。从此，高斯函数成为了数学界的一个重要工具。

三、高斯函数的应用：无处不在的数学魔法

高斯函数的应用范围非常广泛，几乎涵盖了数学的各个领域。以下是一些高斯函数的典型应用：

1. 统计学：高斯函数是正态分布的密度函数，它描述了复杂随机变量和的有限概率分布。在现实生活中，很多看似复杂的数据其实都可以用一个简单的高斯模型来近似表示，比如人的身高、体重、考试成绩分布等。

2. 量子力学：高斯函数是量子谐振子基态的波函数，是计算化学中分子轨道的线性组合的基础。

3. 图像处理：高斯函数在图像处理中用作预平滑核，是尺度空间表示的重要组成部分。它可以帮助我们处理图像噪声和边缘检测等问题。

4. 光学：在光学和微波系统中，高斯波束的应用也是常见的。

5. 量子场论：高斯函数与量子场论中的真空态相关。

四、高斯函数的数学魅力：从对称性到可积性

高斯函数具有许多独特的数学性质，使其在数学界备受青睐。以下是一些高斯函数的数学魅力：

1. 对称性：高斯函数在横轴上关于其中心点对称，这表明函数在中心点两侧的形状是完全一致的。

2. 单峰性：在其定义域内，高斯函数只有一个极大值点位于原点处。

3. 快速衰减性：随着距离中心点的增加，高斯函数的值迅速减小。

4. 可积性：高斯函数在整个实数范围内积分结果等于1。

5. 无限可导：高斯函数在整个实数域内是无限可导的，这意味着它在理论上具有无限平滑的特性。

这些数学性质使得高斯函数成为描述自然界中许多现象的理想模型之一。

五、：高斯函数，数学世界的“钟形曲线”奇遇记

高斯函数，这个数学界的“钟形曲线”奇遇记，以其独特的魅力和广泛的应用，成为了数学世界中的一颗璀璨明珠。让我们一起走进高斯函数的世界，感受数学的神奇与美妙吧！